LeetCode Hot100 -6

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

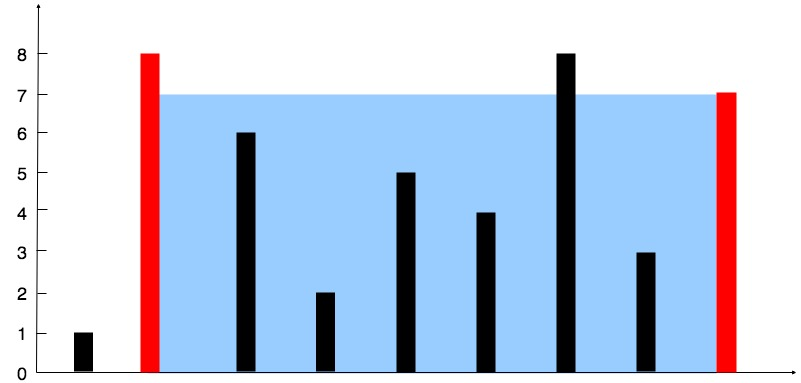
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

常规做法：

通过两层循环枚举，找出所有可能性，得出最大面积。复杂度O(n²)，10^5*2超出时限要求。

	public int maxArea(int[] height) {
		int n = height.length;
		int mx = 0;
		for (int i = 0 ; i < n ; i++) {
			for (int j = i + 1 ; j < n ; j++) {
				mx = Math.max(mx, Math.min(height[i], height[j]) * (j - i));
			}
		}
		return mx;
	}

双指针做法：

通过双指针的滑动，当大边保持不动时，让小边变大，会使整个面积总体变大。复杂度O(n)。

注：原理是，如果不改变小边的高度，那么总体面积不会超出x*t，不如去尝试改变小边。即短板效应。

	public int maxArea(int[] height) {
		int n = height.length;
		int i = 0, j = n - 1;
		int mx = 0;
		while (i < j) {
			mx = Math.max(mx, Math.min(height[i], height[j]) * (j - i));
			if (height[i] < height[j]) {
				i++;
			}
			else {
				j--;
			}
		}
		return mx;
	}